1 − 2 + 3 − 4 + ⋯

Grafički prikaz prvih 15.000 parcijalnih suma reda 0 + 1 − 2 + 3 − 4 + ...

1 − 2 + 3 − 4 + · · · je beskonačan red u matematici, koji obuhvata uzastopne prirodne brojeve sa naizmeničnim znacima. Suma prvih $m$ članova reda može da se napiše kao:

$1-2+3-4+\cdots +m(-1)^{m-1}=\sum _{n=1}^{m}n(-1)^{n-1}.$

Ovaj beskonačni niz divergira, što znači da redosled njegovih parcijalnih suma (1, −1, 2, −2, …), ne teži ka krajnjim granicama. Međutim, sredinom 18. veka, Leonard Ojler je napisao sledeće, što je kasnije okarakterisao kao paradoksalno:

$1-2+3-4+\cdots ={\frac {1}{4}}\!\,.$

Matematička metoda koja bi objasnila ovu jednačinu, razvijena je mnogo kasnije. Počev od 1890. godine, Ernesto Čezaro, Emil Borel i drugi matematičari ispitivali su postojeće metode za određivanje sume divergentnih redova — uključujući i nova tumačenja Ojlerovih pokušaja. Korišćenjem mnogih od ovih metoda za izračunavanje sume reda 1 − 2 + 3 − 4 + · · · dovelo je do konačnog rezultata koji je iznosio ¹⁄₄. Čezarovo sumiranje je jedna od retkih metoda pomoću kojih ne možemo odrediti iznos 1 − 2 + 3 − 4 + · · ·, već se moramo koristiti jačim metodama, kao što je Abelovo sumiranje.

Red 1 − 2 + 3 − 4 + · · · je mnogo sličan Grandijevom redu 1 − 1 + 1 − 1 + · · ·, a Ojler je tretirao ova dva posebna slučaja kao 1 − 2ⁿ + 3ⁿ − 4ⁿ + · · · za proizvoljno n. Dalja istraživanja vremenom su dovela do drugih funkcija, koje su danas poznate kao Rimanova zeta-funkcija i Dirihleova eta-funkcija.

Divergentnost

Članovi reda (1, −2, 3, −4, ...) ne teže ka 0, te 1 − 2 + 3 − 4 + · · · divergira primenom testa opšteg člana. Za dalje razmatranje, bilo bi korisno da se odredi divergencija osnovnog nivoa. Po definiciji, konvergencija ili divergencija beskonačnog reda uslovljena je konvergencijom ili divergencijom reda parcijalnih suma. Shodno tome, parcijalne sume reda 1 − 2 + 3 − 4 + · · · su:

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

…

$\sum _{n=1}^{m}(-1)^{n-1}n\;\;={\frac {(-1)^{m-1}(2m+1)+1}{4}}$

Ovaj red je važan zbog prisustva svakog celog broja — čak i 0, ako računamo praznu parcijalnu sumu — čime je uspostavljena brojivost članova skupa celih brojeva $\mathbb {Z}$. Redosled parcijalnih suma jasno pokazuje da red ne konvergira ka određenom broju (za svaku graničnu vrednost x možemo naći tačku iza koje su sve naredne parcijalne suma van intervala [x-1, x+1]), te stoga 1 − 2 + 3 − 4 + · · · divergira.

Heuristički pristup sumiranja

Stabilnost i linearnost

Budući da članovi 1, −2, 3, −4, 5, −6, ... slede jednostavne zakonitost, red 1 − 2 + 3 − 4 + ... je moguće transformisati premeštanjem i dodavanjem člana na član, sa ciljem da mu se pripiše neko numeričko značenje. Ako izraz s = 1 − 2 + 3 − 4 + ... za neki dati broj s ima smisla, onda sledeće formalne transformacije ukazuju na to da je s = ¹⁄₄:

${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$

Dodavanjem četiri kopije 1 − 2 + 3 − 4 + ..., koristeći samo premeštanje i dodavanje člana na član, daje za rezultat 1.

Zbog toga, $s={\frac {1}{4}}$. Ovo izvođenje je grafički predstavljeno na crtežu sa desne strane.

Iako 1 − 2 + 3 − 4 + ... nema sumu u uobičajenom smislu, jednačina s = 1 − 2 + 3 − 4 + ... = ¹⁄₄ daje najbolji odgovor na to da li ta suma može da se odredi. Uopštena definicija „sume“ divergentnog reda naziva se metod sumiranja, koji omogućava izračunavanje sume nekoliko podskupova svih mogućih redova. Postoje brojne metode za opšte sumiranje redova, a neke od njih sadrže neke od osobina običnog sumiranja redova. U stvari, gore je dokazano da se korišćenjem bilo kog metoda za sumiranje koji je linearan i stabilan za rezultat reda 1 − 2 + 3 − 4 + ... dobija ¹⁄₄. Tačnije:

${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+&(-2+3-4+\cdots )&{}+1-2&+(3-4+5\cdots )\\&=&0+&(-2+3)+(3-4)+(-4+5)+\cdots \\2s&=&&1-1+1-1\cdots \end{array}}$

primena ovog metoda daje i rešenje sume Grandijevog reda, 1 − 1 + 1 − 1 + ... = ¹⁄₂.

Košijev proizvod

Godine 1891, Ernesto Čezaro izrazio je nadu da će divergentni redovi biti uključeni u kalkulus, ukazujući na sledeće:

„ Neki pišu (1 − 1 + 1 − 1 + ...)² = 1 − 2 + 3 − 4 + ... i tvrde da su dve strane jednake ¹⁄₄. ” — Ernesto Čezaro

Za Čezara, ova jednačina predstavlja primenu teoreme koju je objavio godinu pre, te se može smatrati prvom teoremom u istoriji sumiranja divergentnih redova. Detalji ovog metoda za sumiranje su prikazani dole; osnovna ideja je da 1 − 2 + 3 − 4 + ... jeste Košijev proizvod 1 − 1 + 1 − 1 + ... i 1 − 1 + 1 − 1 + ....

Košijev proizvod dva beskonačna reda je definisan, čak iako su ta dva reda divergentna. U slučaju gde je Σa_n = Σb_n = Σ(−1)ⁿ, uslovi Košijevog proizvoda dati su konačnim dijagonalnim sumama:

${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$

Zatim, proizvod reda je:

$\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .$

Na taj način, metod za sumiranje koji sadrži Košijev proizvod dva reda i daje sumu 1 − 1 + 1 − 1 + ... = ¹⁄₂, takođe daje sumu 1 − 2 + 3 − 4 + ... = ¹⁄₄. Sa rezultatom dobijenim u prethodnom odeljku, ovo podrazumeva jednakost između sumiranja 1 − 1 + 1 − 1 + ... i 1 − 2 + 3 − 4 + ... sa metodama koje su linearne, stabilne i sadrže Košijev proizvod.

Čezarova teorema je prefinjen primer. Red 1 − 1 + 1 − 1 + ..., prema Čezaru, može da bude sumiran i zove se (C, 1)-sumirački, dok red 1 − 2 + 3 − 4 + ... zahteva dublju primenu Čezarove teoreme, i zove se (C, 2)-sumirački. Budući da su svi oblici Čezarove teoreme linearni i stabilni, vrednosti sume su one koje smo prethodno izračunali.

Posebne metode

Čezaro i Helder

Podaci za sumu (H, 2) od ¹⁄₄

Za izračunavanje Čezarove sume (C, 1) za 1 − 2 + 3 − 4 + ..., ako postoji, neophodno je da se prvo izračuna aritmetička sredina parcijalnih suma reda. Parcijalne sume su:

1, −1, 2, −2, 3, −3, ...,

a aritmetička sredina ovih parcijalnih suma:

$1,\ 0,\ {\frac {2}{3}},\ 0,\ {\frac {3}{5}},\ 0,\ {\frac {4}{7}},\ \dots$.

Pošto ovaj red ne konvergira, samim tim 1 − 2 + 3 − 4 + ..., prema Čezaru, ne može da se sumira.

Postoje dve poznate generalizacije Čezarovog sumiranja — konceptualno jednostavnija metoda jeste ona koja se sastoji od niza (H, n) metoda za prirodne brojeve n. Suma (H, 1) je suma po Čezaru, a metode višeg reda ponavljaju izračunavanje. U navedenom primeru, parne srednje vrednosti konvergiraju do ¹⁄₂, dok sve neparne srednje vrednosti su jednake 0; dakle, srednje vrednosti srednjih vrednosti se međusobno približavaju vrednostima između 0 i ¹⁄₂, odnosno do ¹⁄₄. Stoga, red 1 − 2 + 3 − 4 + ... ima sumu (H, 2) koja iznosi ¹⁄₄.

Oznaka „H“ predstavlja skraćenicu prezimena Ota Heldera (nem. Otto Hölder), koji je 1882. godine bio prvi koji je dokazao ono što matematičari danas smatraju vezom između Abelovog sumiranja i (H, n) sumiranja. Red 1 − 2 + 3 − 4 + ... je bio prvi primer koji je upotrebljen u tu svrhu. Činjenica da ¹⁄₄ je suma (H, 2) od 1 − 2 + 3 − 4 + ... potvrđuje da je ovo Abelova suma, takođe; ovo je direktno dokazano ispod.

Druga česta generalizacija Čezarovog sumiranja jeste niz od (C, n) metoda. Već je dokazano da sumiranje (C, n) i sumiranje (H, n) uvek daje isti rezultat, ali ona zapravo imaju različite istorijske pozadine. Godine 1887, Čezaro je bio blizu definisanja (C, n) sumiranja, ali je dao samo nekoliko primera. Konkretno, sumirao je 1 − 2 + 3 − 4 + ..., i dobio rezultat ¹⁄₄ metodom koja se može preformulisati kao (C, n), ali koja u to vreme nije bila priznata. Formalno je definisao (C, n) metode 1890. godine, sa ciljem da potkrepi svoju teoremu da Košijev proizvod sume reda (C, n) i sume reda (C, m) je jednak sumi (C, m + n + 1).

Abelovo sumiranje

Izvodi iz 1−2x+3x²+...; 1/(1 + x)²; i granične vrednosti u tački 1

U izveštaju iz 1749. godine, Leonard Ojler je priznao da red divergira, ali ipak se spremao da izračuna njegovu sumu:

„ Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. ”

Ojler je nekoliko puta predlagao generalizaciju pojma „suma reda“. U slučaju 1 − 2 + 3 − 4 + ..., njegove ideje su slične onome što je danas poznato kao Abelovo sumiranje:

„ Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. ”

Postoji mnogo načina da se vidi, bar za apsolutne vrednosti $|x|<1$, da Ojler je u pravu:

$1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.$

Moguće je da izvrši proširivanje na desnoj strani Tejlorovog reda ili da se primeni formalni proces deljenja polinoma. Počevši sa leve strane, može da se sledi opšta heuristika prikazana gore i dva puta da se pomnoži sa (1+x) ili da se izvrši kvadriranje geometrijskog reda 1 − x + x² − .... Izgleda da je Ojler, isto tako, predložio diferenciranje poslednjeg reda član po član.

Sa savremene tačke gledišta, red 1 − 2x + 3x² − 4x³ + ... ne definiše funkciju u tački $x=1$, tako da vrednost ne može jednostavno da se zameni u dobijeni izraz. Pošto je funkcija definisana za svako $|x|<1$, može da izračuna granična vrednost, jer $x$ teži $1$, što u suštini predstavlja definiciju Abelovog sumiranja:

$\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

Ojler i Borel

Ojlerovo sumiranje za ¹⁄₂ − ¹⁄₄

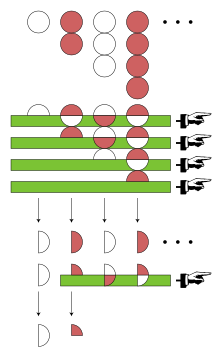
Ojler je primenio drugu metodu za ovaj red, poznatu kao Ojlerova transformacija, što je jedan od njegovih izuma. Da bi izračunali Ojlerovu transformaciju, neophodno je da se počne sa nizom pozitivnih članova — u ovom slučaju sa 1, 2, 3, 4, .... Prvi član ovog niza je označen kao a₀.

Osim toga, neophodno je da se izračuna konačna razlika između članova niza 1, 2, 3, 4, ..., koji je jednak 1, 1, 1, 1, .... Prvi član ovog niza j označen kao Δa₀. Takođe, Ojlerova transformacija zavisi i od razlike razlika, ali sve dalje razlike članova niza 1, 1, 1, 1, ... su jednake sa 0. U tom slučaju, Ojlerova transformacija za red 1 − 2 + 3 − 4 + ... definisana je kao:

${\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.$

U savremenoj terminologiji, kaže se da red 1 − 2 + 3 − 4 + ... može da se sumira po Ojleru, te se pritom dobije suma jednaka ¹⁄₄.

Sumiranje po Ojleru podrazumeva postojanje još jedne vrste sumiranja. Predstavljajući red 1 − 2 + 3 − 4 + ... kao:

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1)$

dovodi do konvergentnog reda u svakoj tački, što se može napisati kao:

$a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).$

Dakle, Borelova suma reda 1 − 2 + 3 − 4 + ... može da se izračuna kao:

$\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.$

Razdvajanje skala

Matematičari Sajčev i Vojčinjski došli su do rešenja 1 − 2 + 3 − 4 + ... = ¹⁄₄ primenom dva fizička principa — infinitezimalne relaksacije i razdvajanje skala. Preciznije, ovi principi kasnije će dovesti do utvrđivanja široke porodice „metoda za φ-sumiranje“, koji svi za sumu daju rezultat ¹⁄₄:

• Ako φ(x) je funkcija čiji su prvi i drugi izvod kontinuirani i integrabilni u intervalu (0, ∞), tako da φ(0) = 1 i granične vrednosti od φ(x) i xφ(x) za +∞ su jednaki 0, onda:

$\lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.$

Ovaj rezultat je generalizacija Abelovog sumiranja, koji se dobija uvođenjem zamene φ(x) = exp(−x). Opšta tvrdnja može da se dokaže grupisanjem članova reda u parove preko $m$ i transformacijom izraza u Rimanov integral. Kada se radi o poslednjem koraku, dokaz za 1 − 1 + 1 − 1 + ... sadrži primenu Lagranžove teoreme za srednju vrednost, ali u ovom slučaju zahteva primenu Lagranžovog oblika napredne Tejlorove teoreme.

Generalizacija

Odlomak 233. strane iz E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. Ojler sumira slične redove, oko 1755.

Trostruki Košijev proizvod reda 1 − 1 + 1 − 1 + ... iznosi 1 − 3 + 6 − 10 + ..., odnosno naizmenični red trouglastih brojeva, čija je Abelova i Ojlerova suma jednaka ¹⁄₈. Četvorostruki Košijev proizvod reda 1 − 1 + 1 − 1 + ... iznosi, ipak, 1 − 4 + 10 − 20 + ..., što predstavlja naizmenični red tetraedalnih brojeva, čija je Abelova suma jednaka ¹⁄₁₆.

Druga generalizacija reda 1 − 2 + 3 − 4 + ... na nešto drugačiji način jeste red 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... za ostale vrednosti n. U slučaju da n ima vrednost pozitivnog broja, redovi ovog tipa imaju sledeće Abelove sume:

$1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}$

gde su B_n Bernulijevi brojevi. Kada je n paran broj, jednačina se svodi na:

$1-2^{2k}+3^{2k}-\cdots =0.$

Poslednja suma postala je Abelov predmet podsmeha, koji je 1826. godine zapisao sledeće:

„ Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. ”

Čezarov učitelj, Ežen Šarl Katalan, takođe je ponižavao divergentne redove. Pod njegovim uticajem, Čezaro je „uslovne formule“ za 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... prvobitno okarakterisao kao „apsurdne jednakosti“, a 1893. godine izrazio je mišljenje — uobičajeno za to vreme — da su formule pogrešne, ali i na neki način korisne. Konačno, u svom delu Sur la multiplication des séries iz 1890. godine, Čezaro je primenio savremeni pristup, počev od definicija.

Redovi su predmet proučavanja i za vrednosti n koje nisu celi brojevi, koji sačinjavaju Dirihleovu eta-funkciju. Deo Ojlerovog zanimanja za izučavanje redova povezanih sa redom 1 − 2 + 3 − 4 + ... bila je funkcionalna jednačina za eta-funkciju, što direktno dovodi do funkcionalne jednačine za Rimanovu zeta-funkciju. Ojler je već postao poznat po pronalaženju vrednosti ovih funkcija sa pozitivnim parnim brojevima — uključujući i Bazelski problem — a pokušavao je da pronađe vrednosti i za pozitivne neparne brojeve — uključujući i Aperijevu konstantu — problem koji je ostao nerešen i neobjašnjiv do danas. Sa Ojlerovim metodama je lakše raditi sa eta-funkcijama, zbog toga što je Abelovo sumiranje njegovog Dirihleovog reda uvek moguće. S druge strane, Dirihleov red sa zeta-funkcijama teže se sumira, jer taj red divergira. Tako na primer, red 1 − 2 + 3 − 4 + ... u zeta-funkciji jeste nenaizmeničan red 1 + 2 + 3 + 4 + ..., koji ima duboke primene u savremenoj fizici, ali zahteva primenu mnogo jače metode za izračunavanje njegovih suma.

Literatura

• Beals, Richard (2004). Analysis: an introduction. Cambridge UP. ISBN 978-0-521-60047-7. 
• Davis, Harry F. (1989). Fourier Series and Orthogonal Functions. Dover. ISBN 978-0-486-65973-2. 
• Euler, Leonhard; Willis, Lucas; Osler, Thomas J (2006). „Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series”. The Euler Archive. Pristupljeno 19. 12. 2012. 
• Ferraro, Giovanni (1999). „The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics”. Archive for History of Exact Sciences. 54 (2): 101—135. S2CID 119766124. doi:10.1007/s004070050036. 
• Grattan-Guinness, Ivor (1970). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 978-0-262-07034-8. 
• Hardy, G.H. (1949). Divergent Series. Clarendon Press. LCCN 9175377 . 
• Kline, Morris (1983). „Euler and Infinite Series”. Mathematics Magazine. 56 (5): 307—314. JSTOR 2690371. doi:10.2307/2690371. 
• Knopp, Konrad (1956). Infinite Sequences and Series. Dover Publications. ISBN 978-0-486-60153-3. 
• Lavine, Shaughan (1994). Understanding the Infinite. Harvard UP. ISBN 978-0-674-92096-5. 
• Markushevich, A.I. (1967). Series: fundamental concepts with historical exposition. Hindustan Pub. Corp. LCCN 6817528 . 
• Saichev, A.I; Woyczyński, W.A (1996). Distributions in the physical and engineering sciences, Volume 1. Birkhaüser. ISBN 978-0-8176-3924-2. 
• Tucciarone, John (1973). „The development of the theory of summable divergent series from 1880 to 1925”. Archive for History of Exact Sciences. 10 (1–2): 1—40. S2CID 121888821. doi:10.1007/BF00343405. 
• Vretblad, Anders (2003). Fourier Analysis and Its Applications. Springer. ISBN 978-0-387-00836-3. 
• Weidlich, John E. (1950). Summability methods for divergent series. Stanford M.S. theses. OCLC 38624384. 

Spoljašnje veze

• Jednačine i formule za 1 − 2 + 3 − 4 + ...
• Mathematics Magazine (1983) — Euler and Infinite Series
• Series — Wolfram's Mathworld